1.
a. Bij x = 3 hoort y = 15
b. Bij x = 0 hoort y = -3
c. Bij x = -4 hoort y = 29
2.
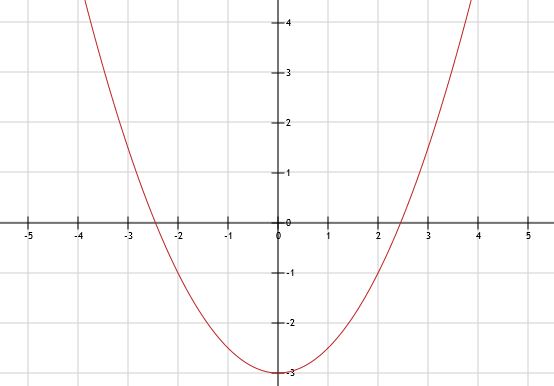
a. Het is een dalparabool. Er staat een positief getal voor de x2.
b. x = 3 invullen, levert y = 0,5 x (3)2 - 3 = 0,5 x 9 - 3 = 4,5 - 3 = 1,5
c. Zie afbeelding
3.
Tip:
Als het getal voor de x2:
- positief is, dan is het een dalparabool
- negatief is, dan is het een bergparabool
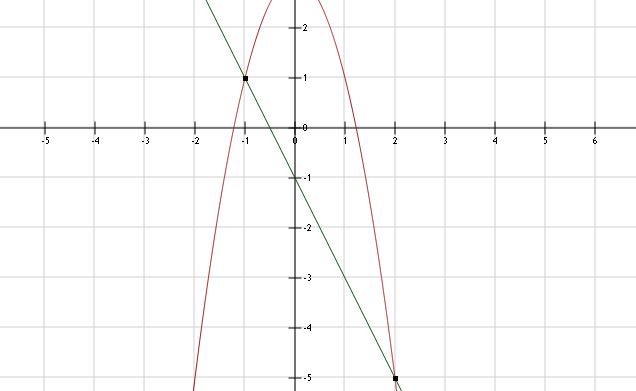
a. y = -2x2 + 3 is een parabool. De andere formule is een rechte lijn.
b. Zie afbeelding.
c. Coördinaten van de 2 snijpunten zijn: (-1,1) en (2,-5).
4.
Tip:
Bij y = ax2 en a > 0 dan is het een dalparabool.
Bij y = ax2 en a < 0 dan is het een bergparabool.
a. Bij y = x2 hoort de groene grafiek.
Bij y = 0,5x2 hoort de rode grafiek.
Bij y = -x2 hoort de blauwe grafiek.
Bij y = -0,25x2 hoort de zwarte grafiek.
b. De dalparabolen zijn: II en IV
De bergparabolen zijn: I en III
5.
Tip:
Om te bepalen of een punt P(x,y) op een parabool ligt, vul dit punt in en kijk of het klopt!
a.
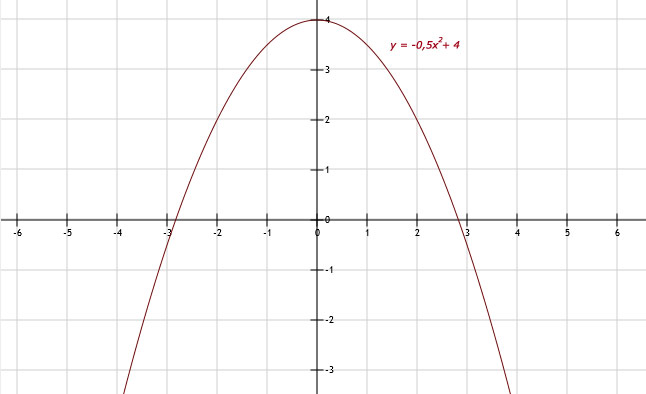
x -3 -2 -1 0 1 2 3 y -0,5 2 3,5 4 3,5 2 -0,5
b. Het hoogste punt is de top. Dat is T(0,4).
c. Invullen x = 18 levert: -0,5 x (18)2 + 4 = -0,5 x 324 + 4 = -158
d. Invullen x = 26 levert: -0,5 x (26)2 + 4 = -0,5 x 676 + 4 = -334. Ja, punt ligt op de grafiek.
e. Invullen x = 6 levert: -0,5 x (6)2 + 4 = -0,5 x 36 + 4 = -14, dus dit punt ligt op de grafiek.
Invullen x = 16 levert: -0,5 x (16)2 + 4 = -0,5 x 256 + 4 = -124, dus dit punt ligt niet op de grafiek.
Invullen x = -5 levert: -0,5 x (-5)2 + 4 = -0,5 x 25 + 4 = -8,5, dus dit punt ligt op de grafiek.
Invullen x = -12 levert: -0,5 x (-12)2 + 4 = -0,5 x 144 + 4 = -68, dus dit punt ligt op de grafiek.
6.
Tip:
Snijpunt y-as, dus x = 0, dus 0 invullen in de formule ofwel f(0).
a. Invullen x = 0 levert y = -1. Dus A(0,-1).
b.
Invullen x = 7 levert: y = 0,25 x (7)2 - 1 = 11,25, dus dit punt ligt op de grafiek.
Invullen x = 10 levert: y = 0,25 x (10)2 - 1 = 24, dus dit punt ligt niet op de grafiek.
Invullen x = -8 levert: y = 0,25 x (-8)2 - 1 = 15, dus dit punt ligt op de grafiek.
7.
Tip:
Is het getal voor de x2 positief dan is het een dalparabool.
Is het getal voor de x2 negatief dan is het een bergparabool.
a. y = 0,25x2 - 1 door (-4,p) levert:
p = 0,25⋅(-4)2 - 1
p = 0,25⋅16 - 1
p = 4 - 1 = 3
p = 3
b. y = -3x2 + 8 door (5,q) levert:
q = -3⋅(5)2 + 8
q = -3⋅25 + 8
q = -67
c. y = ax2 door (2,8) levert:
8 = a⋅(2)2
8 = 4a
a = 2
d. y = -x2 + b door (-4,18) levert:
b = 34
8.
Tip:
Bij x = 0 is de hoogte gelijk aan 0.
a.
Het laagste punt is bij x = 0. Dit invullen levert: h = 0,03 x 02 = 0 meter.
Het hoogste punt is bij x = 4,5. Dit invullen levert: h = 0,03 x 4,52 = 0,6075 meter.
Dit levert een verschil in mm van: 607,5 mm.
b.
x = 2,25 invullen levert: h = 0,03 x 2,252 = 0,151875 meter.
Dit is dus ongeveer 15,2 cm.
Dus het midden ligt op een hoogte van 15,2 cm.
Dus de skeeler bevindt zich links van het midden.
9.
Tip:
Het punt A ligt bij x = 80.
a.
x 0 30 60 90 h 25 29,5 43 65,5
b.
Dat is bij x = 0. Dit is bij h = 25 meter.
c.
Het hoogste punt zit bij x = 120. Dit levert: h = 0,005 x 1202 + 25 = 97 (meter).
Het laagste punt zit bij x = 0. Dit levert: h = 0,005 x 02 + 25 = 25 (meter).
Het verschil is dus: 97 - 25 = 72 meter.
d.
x = 80 invullen, levert: h = 0,005 x 802 + 25 = 57 (meter).
Dus de lengte van AB is gelijk aan 57 meter.
10.
Tip:
AB = 80 meter, dan krijg je dus 2 stukken van 40 meter. Je vindt dit terug bij x = -40 en x = 40.
a.
Bereken eerst x = 0. Dit levert: h = 0,00625 x 02 + 5 = 5 meter.
Dus de rode kabel hangt 5 + 4 = 9 meter boven het water.
b.
x = 40 invullen, levert: h = 0,00625 x 402 + 5 = 15 meter.
c.
De palen zitten bij x = -30, x = -20, x = -10, x = 0, x = 10, x = 20 en x = 30.
x = -30 invullen, levert: h = 0,00625 x (-30)2 + 5 = 10,625 meter.
x = -20 invullen, levert: h = 0,00625 x (-20)2 + 5 = 7,5 meter.
x = -10 invullen, levert: h = 0,00625 x (-10)2 + 5 = 5,625 meter.
x = 0 invullen, levert: h = 0,00625 x (0)2 + 5 = 5 meter.
x = 10 invullen, levert: h = 0,00625 x (10)2 + 5 = 5,625 meter.
x = 20 invullen, levert: h = 0,00625 x (20)2 + 5 = 7,5 meter.
x = 30 invullen, levert: h = 0,00625 x (30)2 + 5 = 10,625 meter.
Alles opgeteld, levert: 52,5 meter.
11.
Tip:
x is de afstand die je loopt vanaf de verticale lijn h naar links of rechts.
a. Vul in x = 50 levert h(50) = 0,01 x 502 + 7 = 32. Dus de pylonen zijn 32 meter hoog.
b. 45 : 2 = 22,5. Vul in x = 22,5 levert h(22,5) = 0,01 x 22,52 + 7 = 12,0625.
Dus de lampjes hangen op een hoogte van ca. 12 meter boven de x-as.
De weg zelf hangt 7 meter boven de x-as (bereken hiertoe x = 0). Dus de lampjes hangen 12,0625 - 7 = 5,0625 meter boven de weg.
c. Vul in x = 25 levert h(25) = 0,01 x 252 + 7 = 13,25. Dus minder dan 50 meter uit elkaar.





REACTIES
:name
:name
:comment
1 seconde geleden